Vector Math & Texture Mapping
Ok this is the little I understand on how texture mapping can be done
(with nice pictures :))
We are looking for a corespondence between a point on a picture and a
point on the screen. I assume we do know that if we have a point in
3d space we can get the point on the screen . We'll start from:
p= x*k1/z (1)
q= y*k2/z (2)
(p,q) is the point in 2d screen,
k1 and k2 are some constatns, usually related to the screen ratio
(if you had a square screen then they would be equal)
(x,y,z) are the coordinates of the point in 3d space
we can express a point that is on a plane two ways
1) with x,y,z -- the coordinates of the point. We could also write this as
/ x \
| y |
\ z /
2) first we'd better have a picture (which was harder to make then I
thought btw):
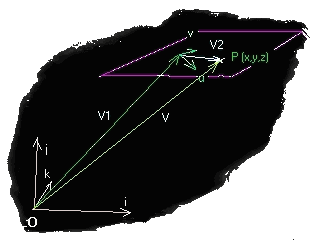 (sorry about the picture quality, netscape converted it to low
quality without me asking it)
I assume you know (or accept) some vector concepts. I'll bold
vectors and have numbers normal (un-bolded)
Here we have:
V = V1 + V2
Back to another picture. It's a view of the plane on which the
point we're interested in is (2d, no more 3d):
(sorry about the picture quality, netscape converted it to low
quality without me asking it)
I assume you know (or accept) some vector concepts. I'll bold
vectors and have numbers normal (un-bolded)
Here we have:
V = V1 + V2
Back to another picture. It's a view of the plane on which the
point we're interested in is (2d, no more 3d):
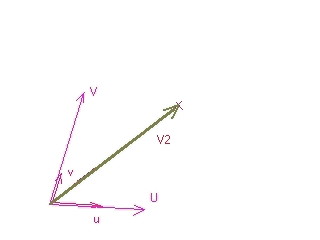 Here V2 is U+V ('cause that's how I took U+V). But U can be
written like something like 2*u and V could be written something
like 3*v. Now in stead of actual numbers we'll use u and v. So we have
V2=u*u+v*v
Note that u is a vector, but u is only a number.
BTW: these are the numbers we are looking for (u and v are the
texture coordinates)
So what we end up with is
V=V1+V2=V1+ u*u + v*v
But each vector can be written something like
V=2.3*i + 3.5*j + 4*k
, with i, j, and k forming the basis of the 3d space we're working in ,
or (i've seen it like this for the first time in programming docs) :
/ 2.3 \
V= | 3.5 |
\ 4 /
so for what we have above we can re-write as:
/ V1x \ /ux \ / vx \
V= V1 + V2 = | V1y | + u * |uy | + v * | vy |
\ V1z / \uz / \ vz /
So where did we start out? We now have
/ x \ / V1x \ /ux \ / vx \
| y | = | V1y | + u * | uy | + v * | vy |
\ z / \ V1z / \uz / \ vz /
This is actually three equations (take the top of each one and you
get an equation). The things we don't know in there are x, y, z.
But we take the x and y from the
(1) and (2) formulas at the beginning of the doc.
Then we end up with three equations with three unknowns: z,u,v.
We solve for u and v.
Some (programming) reality breaks:
We can get V1 , ux,uy,uz and vx,vy,vz. If we have 3 points (which
determine a plane) we can get these values.
If anybody has any questions/opinions on what I've said here I'd be
glad to answer/discuss them. Hope this does somebody some good.
Void lon iXaarii
Here V2 is U+V ('cause that's how I took U+V). But U can be
written like something like 2*u and V could be written something
like 3*v. Now in stead of actual numbers we'll use u and v. So we have
V2=u*u+v*v
Note that u is a vector, but u is only a number.
BTW: these are the numbers we are looking for (u and v are the
texture coordinates)
So what we end up with is
V=V1+V2=V1+ u*u + v*v
But each vector can be written something like
V=2.3*i + 3.5*j + 4*k
, with i, j, and k forming the basis of the 3d space we're working in ,
or (i've seen it like this for the first time in programming docs) :
/ 2.3 \
V= | 3.5 |
\ 4 /
so for what we have above we can re-write as:
/ V1x \ /ux \ / vx \
V= V1 + V2 = | V1y | + u * |uy | + v * | vy |
\ V1z / \uz / \ vz /
So where did we start out? We now have
/ x \ / V1x \ /ux \ / vx \
| y | = | V1y | + u * | uy | + v * | vy |
\ z / \ V1z / \uz / \ vz /
This is actually three equations (take the top of each one and you
get an equation). The things we don't know in there are x, y, z.
But we take the x and y from the
(1) and (2) formulas at the beginning of the doc.
Then we end up with three equations with three unknowns: z,u,v.
We solve for u and v.
Some (programming) reality breaks:
We can get V1 , ux,uy,uz and vx,vy,vz. If we have 3 points (which
determine a plane) we can get these values.
If anybody has any questions/opinions on what I've said here I'd be
glad to answer/discuss them. Hope this does somebody some good.
Void lon iXaarii
(sorry about the picture quality, netscape converted it to low quality without me asking it) I assume you know (or accept) some vector concepts. I'll bold vectors and have numbers normal (un-bolded) Here we have: V = V1 + V2 Back to another picture. It's a view of the plane on which the point we're interested in is (2d, no more 3d):
Here V2 is U+V ('cause that's how I took U+V). But U can be written like something like 2*u and V could be written something like 3*v. Now in stead of actual numbers we'll use u and v. So we have V2=u*u+v*v Note that u is a vector, but u is only a number. BTW: these are the numbers we are looking for (u and v are the texture coordinates) So what we end up with is V=V1+V2=V1+ u*u + v*v But each vector can be written something like V=2.3*i + 3.5*j + 4*k , with i, j, and k forming the basis of the 3d space we're working in , or (i've seen it like this for the first time in programming docs) : / 2.3 \ V= | 3.5 | \ 4 / so for what we have above we can re-write as: / V1x \ /ux \ / vx \ V= V1 + V2 = | V1y | + u * |uy | + v * | vy | \ V1z / \uz / \ vz / So where did we start out? We now have / x \ / V1x \ /ux \ / vx \ | y | = | V1y | + u * | uy | + v * | vy | \ z / \ V1z / \uz / \ vz / This is actually three equations (take the top of each one and you get an equation). The things we don't know in there are x, y, z. But we take the x and y from the (1) and (2) formulas at the beginning of the doc. Then we end up with three equations with three unknowns: z,u,v. We solve for u and v. Some (programming) reality breaks: We can get V1 , ux,uy,uz and vx,vy,vz. If we have 3 points (which determine a plane) we can get these values. If anybody has any questions/opinions on what I've said here I'd be glad to answer/discuss them. Hope this does somebody some good. Void lon iXaarii