Void lon iXaarii
fascinated by creation
Point Position Relative to a Plane
Why I wrote this doc
I was thinking one day about implementing determining the position of a point with respect to a plane today (to use it for some space partitioning) when I realized none of the docs I had covered something as basic as this and I knew nothing about it except same vague memory that I once read somewhere something like that you only have to insert the x,y,z of that point into the left side of the plane equation A*x+B*y+C*z+D=0 equation and if it was greater than 0 that meant it was on one side, if it was 0 it was on the plane and if it was less than 0 it was on the other side. But I hate implementing guesses (unless they’re backed by intuition) so I tried to find something I knew and trusted. I didn’t even trust the plane equation (doesn’t feel very intuitive to me). So, using some stuff I read in a doc called “Point-Normal form for a plane” and my once sain knowledge of vectors I found some proof that satisfied me as far as finding the position of a point with respect to a plane. This is it.
Preliminaries:
I will start from (don’t know how to proove): the dot product “.” is distributive and is defined as:
A . B = A * B * cos(alpha)
where A and B are the lengths of the vectors A and B and alpha is the small angle between the two vectors.
So, since every vector (starting in the origin of space) can be written as
P = Px*i + Py*j + Pz*k
where i, j and k are the unit vectors on the 3 axises of 3d space and Px, Py and Pz are the lengths of the vector along the 3 axises (it’s projections on these) for two vectors P and N we have:
P . N = (Px*i+Py*j+Pz*k) . (Nx*i+Ny*j+Nz*k)= Px*Nx + Py*Ny + Pz*Nz
because
i.i=j.j=k.k=1*1*cos(0 degrees)=1
and
i.j=i.k=j.k=1*1*cos(90 degrees)=0
and now that we’re over with the preliminaries, on to
The main stuff
I’ll show that
N . P = D
is a good way to represent a plane. N is a vector normal to the plane we are talking about, P is a point in this plane and D is a scalar (number).
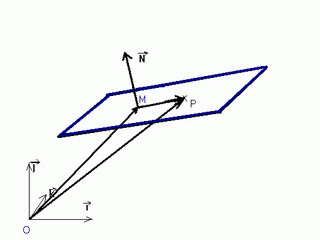
P (who’s just a nickname for OP, the vector who has it’s origin in O and ends in P) can be written as the vectorial sum of vectors OM and MP (vectors going from O to M and respectively M to P). So:
N . P = N . (OM+MP)= N . OM + N . MP
but N . OM is a constant number for any P in the given plane because the lengths of the vectors N and OM are constant and so is the angle between them and N . MP is 0 because the angle between the vectors is 90 degrees. So, indeed, for all points in the plane (and only those) that equation is true. This happens to turn into the known equation of A*x+B*y+C*z=D for a plane if you consider the equation we ended up with in the preliminaries changing some names.
Now imagine the point P moving out of the plane. I’ll try to show that when it’s on one side of the plane then N . P – D is greater than 0 and when it’s on the other side it’s less than 0 (I’ve already shown that it’s equal when it’s in the plane). Going with the above picture:
1) when point P moves above the plane: N . OM is D and N . MP is greater than 0 (because the lengths are always positive and cosinus is positive for an angle between 0 and 90 degrees), so
N . P = N . OM + N . MP – D = D + N . MP – D = N . MP > 0
2) when point P moves below the plane: N . OM is D and N . MP is less than 0 (because the lengths are always positive and cosinus is negative for an angle between 90 and 180 degrees), so
N . P = N . OM + N . MP – D = D + N . MP – D = N . MP < 0